
Другие статьи из рубрики «Дифференцированный платеж»
- Задача №1 (общая сумма выплат)
- Задача №10 (общий размер всех выплат)
- Задача №2 (минимальный срок кредитования)
- Задача №3 (определение срока кредитования)
- Задача №4 (определение срока кредитования)
- Задача №5 (нахождение процентной ставки банка)
- Задача №6 (поиск процентной ставки банка)
- Задача №7 (переплата по кредиту в %-ном отношении)
- Задача №8 (поиск процентной ставки банка)
- Задача №9 (общий размер всех выплат)
|
Содержание: |
Не получается успешно решать задачи на дифференцированные платежи из ЕГЭ по математике?
Всем здравствуйте! Меня зовут Александр. Я - профессиональный репетитор по математике, информатике, программированию, базам данных и алгоритмам. Если коротко, то я - матерый технарь.![]()
Одно из генеральных моих направлений - подготовка школьников к успешной сдаче ЕГЭ по математике и информатике. Потратьте буквально $2-3$ минуты собственного времени и познакомьтесь с отзывами моих учеников. Средний балл моих подопечных на официальном экзамене ЕГЭ составляет $91.35$ из $100$ возможных.
Задачи на дифференцированные платежи из ЕГЭ по математике являются одними из моих любимых. Вообще задания из экономического блока мне кажутся очень интересными и познавательными. Поэтому на своих индивидуальных уроках я с большим удовольствием показываю своим ученикам различные эффективные методики их решения.
Существует по-настоящему лишь $2$ способа подготовки на высоченный итоговый балл ЕГЭ по математике:
Самоподготовка (автодидактирование).
Под началом профессионального репетитора.
Мой контактный номер телефона прописан в шапке данного сайта. Звоните, договаривайтесь о времени проведения и записывайтесь на первый пробный урок.
Условие задачи
В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей?
Решение задачи
Это классическая задача на дифференцированные платежи из ЕГЭ по математике. Почему я так решил? Потому, что есть фраза-маркер, в которой четко дают понять, что размер займа уменьшается равномерно. Вот эта фраза: "В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года".
С кредитной программой мы разобрались! Это очень важный момент. Если вы спутаете тип кредитной программы, то гарантировано получите неправильный результат. Именно по этой причине я настоятельно прошу всех выучить свойства и признаки схемы дифференцированных платежей.
Кстати, напомню, что фундаментально кредитная программа бывает двух видов:
Кредит выплачивается по схеме дифференцированных платежей.
Кредит выплачивается по схеме аннуитетных платежей.
Давайте введем следующие обозначения:
| \(S\) - размер первоначального кредита | \(r\) - процентная ставка банка, выраженная в долях | \(R = 1 + r\) - для удобства расчетов |
| \(n\) - общее количество отчетных периодов | \(i\) - номер текущего отчетного периода | \(\%_{i}\) - размер начисленных банком процентов за конкретный период |
| \(p_{i}\) - размер платежа за конкретный период | \(P\) - общая сумма всех выплат/платежей | \(q\) - ставка банка, выраженная в процентах |
Хочется отметить следующее, что не все выше обозначенные переменные нам потребуются в процессе решении задачи. Но понимать математический смысл вы обязаны каждой из них, если, конечно, не хотите "завалить" экзамен ЕГЭ по математике.![]()
Дальше, давайте рассмотрим под микроскопом следующую фразу: "наибольший годовой платеж составит \(9\) миллионов рублей". В этой фразе содержится наиважнейшая информация, и ваша цель - суметь ее расшифровать. Для этого нужно прекрасно понимать, как устроена математическая модель дифференцированных платежей, а также знать свойства этих платежей.
Как известно, в схеме дифференцируемых платежей самый $1$-ый платеж является наибольшим, а самый последний - наименьшим! Значит, когда говорят про наибольший платеж, нужно подразумевать самый $1$-ый платеж.
Из условия вытекает, что:
| $S = 28$, млн. руб. | $q = 25\%$ | $r = \frac{q}{100} = 0.25$ | $p_{1} = 9$, млн. руб. |
Наша задача определить $P$, то есть общий размер всех платежей/выплат!
Важно! Если вы хотите получить максимальный балл за решение задачи на дифференцированные платежи из ЕГЭ по математике, то в своем решении нужно привести вывод соответствуюей математической модели. Поэтому, если плохо знаете принцип работы этой модели - срочно идите ее изучать, зубрить.
Вспомним, что платеж за любой отчетный период формируется из размера начисленных процентов за данный период и равной части первоначального кредита:
$p_{i} = \%_{i} + \frac{S}{n}$ - размер $i$-го платежа.
Ранее мы выяснили, что из условия задачи нам известен размер $1$-го платежа ($i = 1$). Значит, процентная ставка банка $q$ действует на весь стартовый кредит:
$\%_{1} = \frac{n}{n} * S * r = S * r = 28 * 0.25 = 7$, млн. рублей. Тогда:
$p_{1} = \%_{1} + \frac{S}{n} = 7 + \frac{28}{n}$.
А размер $1$-го платежа нам задан, он равен $9$ млн. рублей, тогда решим следующее уравнение:
$7 + \frac{28}{n} = 9$
$\frac{28}{n} = 2$
$2 * n = 28$
$n = 14$.
Оказывается, первоначальный кредит был взят сроком на $14$ лет. При этом все ограничения будут соблюдены. Например, самый наибольший/первый платеж составит $9$ миллионов рублей. Отлично! Идем дальше!
Обратимся к формулам математической модели дифференцируемых платежей и "достанем" наиболее важную из них, а именно формулу, которая позволяет вычислить размер всех платежей:
$P = \frac{S\ *\ r\ * (n\ +\ 1)}{2} + S$.
Подставим все известные величины в эту формулу и получим ответ. Заметьте, что в этой формуле фигурирует переменная $n$, то есть необходимо знать общее количество отчетных периодов. Ее значение мы нашли на предыдущем шаге ($n = 14$).
$P = \frac{28\ *\ 0.25\ *\ (14\ +\ 1)}{2} + 28 = \frac{105}{2} + 28 = 52.5 + 28 = 80.5$, млн.руб.
Готово! Результат получен! Да, получилось нецелое значение, но это и не главное. Хотя в большинстве случаев входные данные в задачах на дифференцированные платежи из ЕГЭ по математике подбираются так, чтобы на выходе образовывалось что-то целое.
Но у любознательных старшеклассников может появиться вполне закономерный вопрос: "А правильный ли ответ?". Очевидно, что, да! ![]() Но ведь нужны какие-то гарантии, верно.
Но ведь нужны какие-то гарантии, верно.
Верификацию полученного результата можно произвести арифметическим способом. То есть вы можете пройтись по всем отчетным периодам, вычисляя соответствующие платежи, размер начисленных банком процентов и т.п.
Но на своих индивидуальных занятиях, совместно с учеником, мы проводим верификацию полученных результатов, посредством математического процессора "MS Excel". Это очень удобный и наглядный вариант проверки решения. Также, построенная таблица обладает хорошим аналитизмом, то есть, анализируя выкладки этой таблицы, становятся понятны многие тонкие моменты, связанные с выплатой кредита.
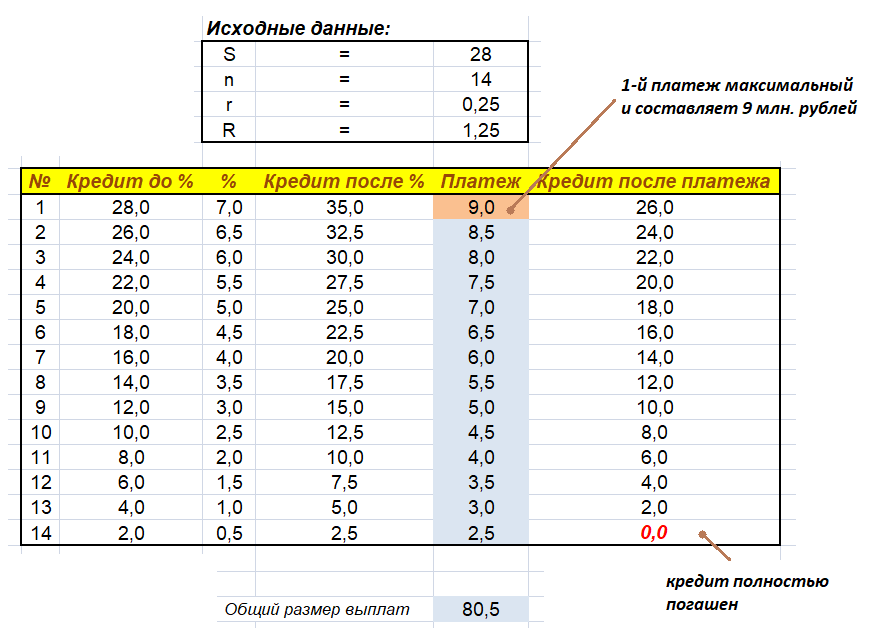
Данная великолепная таблица доказывает правильность нашего алгебраического решения.
Ответ: 80.5
Выводы
Для успешного решения задач на дифференцированные платежи из ЕГЭ по математике нужно знать назубок соответствующую математическую модель. Пока не поймете эту модель, даже не вздумайте пытаться что-то решать из подобного типа заданий.
На официальном экзамене, для получения максимального балла за экономическую задачу, в своем решении приводите, в том числе и вывод математической модели. В этом случае ни один эксперт в процессе проверки не сможет "придраться" к вашим математическим выкладкам.
Внимательно читайте условие задачи и обращайте особое внимание на фразы-маркеры. Это позволит вам выбрать наиболее эффективный способ решения и не ошибиться в выборе кредитной программы.
Решайте задания с применением алгебраического способа, а не арифметического. Хотя оба этих способа уместны, но более профессиональным и продвинутым считается именно алгебраический.
И, пожалуй, одно из главных - нужно любить математику.

Примеры условий реальных задач, встречающихся на ЕГЭ по математике
А сейчас я приведу список из нескольких задач на дифференцированные платежи из ЕГЭ по математике. Вы можете попробовать порешать их самостоятельно. Если будут трудности, то переходите по ссылке "Перейти к текстовому решению" и знакомьтесь полноценным моим решением.
Не забывайте о том, что раздел "Финансовая математика" содержит множество других типов задач: аннуитетные платежи, вклады, простые и сложные проценты, акции и т.д. Также зачастую попадаются комбинированные задачи, где происходит смешение моделей. Хотите во всем этом разбираться? Записывайтесь ко мне на частную подготовку!
|
Пример №1 В мае планируется взять кредит в банке на сумму \(10\) миллионов рублей на \(5\) лет.
Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита? |
|
Пример №2 В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на некоторый срок.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил \(1.8\) миллиона рублей? |
|
Пример №3 В июле планируется взять кредит в банке на сумму \(20\) миллионов рублей на некоторый срок (целое число лет).
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(47\) миллионов рублей? |
|
Пример №4 В июле планируется взять кредит в банке на сумму \(16\) миллионов рублей на некоторый срок (целое число лет).
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(38\) миллионов рублей? |
|
Пример №5 В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на срок \(15\) лет.
Найти \(q\), если известно, что наибольший годовой платеж по кредиту составит не более \(1.9\) миллиона рублей, а наименьший не менее \(0.5\) миллиона рублей. |
|
Пример №6 \(15\) января планируется взять кредит в банке на \(39\) месяцев.
Известно, что общая сумма выплат после полного погашения кредита на \(20\%\) больше суммы, взятой в кредит. Найдите \(q\). |
|
Пример №7 Анатолий взял банковский кредит сроком на \(9\) лет. В конце каждого года общая сумма оставшегося долга увеличивается на \(17\%\), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)? |
|
Пример №8 Анна взяла кредит в банке на срок \(12\) месяцев (\(1\) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется \(q\%\) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется "схемой с дифференцированными платежами"). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на \(13\%\) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть \(q\). |
|
Пример №9 В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей? |
|
Пример №10 \(15\) января планируется взять кредит в банке на \(15\) месяцев.
Известно, что восьмая выплата составила \(108\,000\) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования? |
Все эти задачи на дифференцированные платежи из ЕГЭ по математике решаются достаточно быстро, если вы хорошо знаете, как устроена математическая модель дифференцируемых платежей. Повторю, уже, наверное, раз $10$-ый - разбирайтесь с математической моделью, и будем вам счастье.
Также, время от времени, рекомендую обращаться к этому списку заданий, так как он постоянно обновляется и дополняется, появляются новые условия, а также соответствующие мои математические разборы.
Что-то все равно осталось непонятным? Записывайтесь ко мне на частную подготовку!
Если после прочтения данного материала у вас остались какие-то вопросы, недопонимания, то это некритично, и, даже, вполне логично! Недостаточно пристально рассмотреть одно решение задачи на дифференцированные платежи из ЕГЭ по математике. Нужен комплексный подход!
Я - репетитор-практик, который на своих занятиях, уделяет львиное количество времени конкретным разборам, техникам и эффективным методикам решения. Всевозможной теории полно в глобальной сети Интернет, а экзамен ЕГЭ по математике является практическим, то есть нужно уметь решать, а не знать теоретические изыски.
Мои занятия проходят дистанционно, посредством таких программ, как "Скайп" и "AnyDesk". Подобный формат взаимодействия репетитора с учеником является очень удобным, позволяет задействовать мультимедийные технологии, а также достаточно недорог.
Я достаточно востребованный и известный репетитор по математике и информатике, поэтому, не откладывайте свое решение в долгий ящик. Действуйте прямо сейчас! И не забывайте, что количество ученических мест ограничено, поэтому, завтра свободных мест уже может и не остаться.
Отзывы
моих учеников

Ахматова
Юлия

Булычев
Владимир

Богдан
Игнатьев

Арапов
Александр

Евдокимов
Максим

Потанин
Михаил

Волков
Антон

Шамшуров
Денис

Потапова
Ирина

Владимир
Дятлов

Фомин
Глеб

Орлов
Максим

Леонов
Никос

Агаров
Ярослав

Самуйлов
Кирилл

Воробьев
Станислав

Даниил
Сафонов

Коваленко
Всеволод

Малышев
Евгений

Александров
Михаил
Самые популярные статьи из других рубрик
- Каким образом я выстраиваю конечную стадию проведения индивидуальных уроков по информатике и ИКТ
- Каким образом я выстраиваю основную, то есть центральную стадию проведения индивидуальных уроков по информатике и ИКТ
- Поведение репетитора по информатике в Москве в процессе урока. Репетиторы разные, следовательно, и их поведение тоже различно!






 Закажите
Закажите Смотрите
Смотрите Напишите
Напишите Закажите
Закажите