
Другие статьи из рубрики «Кодирование графической информации»
|
Содержание: |
С трудом получается решать задачи на кодирование графической информации?
Привет! Вы оказались на моем персональном сайте. Меня зовут Александр. По профессии я репетитор по информатике, математике, базам данных и программированию.
Ключевая компетенция моей деятельности - высококвалифицированная подготовка школьников $9-11$-ых классов к успешной сдаче ОГЭ и ЕГЭ по информатике.
Если вам предстоит сдача ЕГЭ по информатике, а вы совсем плохо понимаете такую тему, как "Кодирование графической информации", то я предлагаю вам $2$ пути решения этой проблемы:
Записаться ко мне на частную подготовку.
Готовиться по материалам, опубликованным на этом сайте.
Какой вариант более продуктивный?![]() Разумеется, $1$-ый! Поэтому действуйте прямо сейчас, не откладывайте свое решение в долгий ящик. Дозванивайтесь до меня по номеру, указанному в шапке сайта, и записывайтесь на $1$-й пробный урок.
Разумеется, $1$-ый! Поэтому действуйте прямо сейчас, не откладывайте свое решение в долгий ящик. Дозванивайтесь до меня по номеру, указанному в шапке сайта, и записывайтесь на $1$-й пробный урок.
Даю индивидуальные занятия в различных территориальных форматах:
В настоящий момент практически все мои подопечные занимаются со мной дистанционно, посредством программы "Скайп". Это очень удобно, достаточно недорого и крайне эффективно!
Условие задачи
После преобразования растрового $256$-цветного графического файла в $4$-цветный формат его размер сократился на [$18$ Кбайт].
Каков был размер исходного файла? Ответ получить в [Кбайтах].
Решение задачи
В школе вы должны познакомиться с $3$-мя видами компьютерной графики:
| растровая графика | векторная графика | фрактальная графика |
В заданиях ЕГЭ по информатике, ориентированных на кодирование графической информации, в обязательном порядке сообщают, какого типа изображения обрабатывается.
Эта задача не является исключением.![]() Видим, что в постановке есть такая фраза: "После преобразования растрового ...". Все вопросы сняты! Нам предстоит анализировать классическое растровое изображение. И это очень хорошо!
Видим, что в постановке есть такая фраза: "После преобразования растрового ...". Все вопросы сняты! Нам предстоит анализировать классическое растровое изображение. И это очень хорошо!
Обратите внимание, что изначально нам не задали габариты графического файла, т е мы не знаем, из какого количества пикселей оно состоит. Ведать для успешного решения это и не важно!
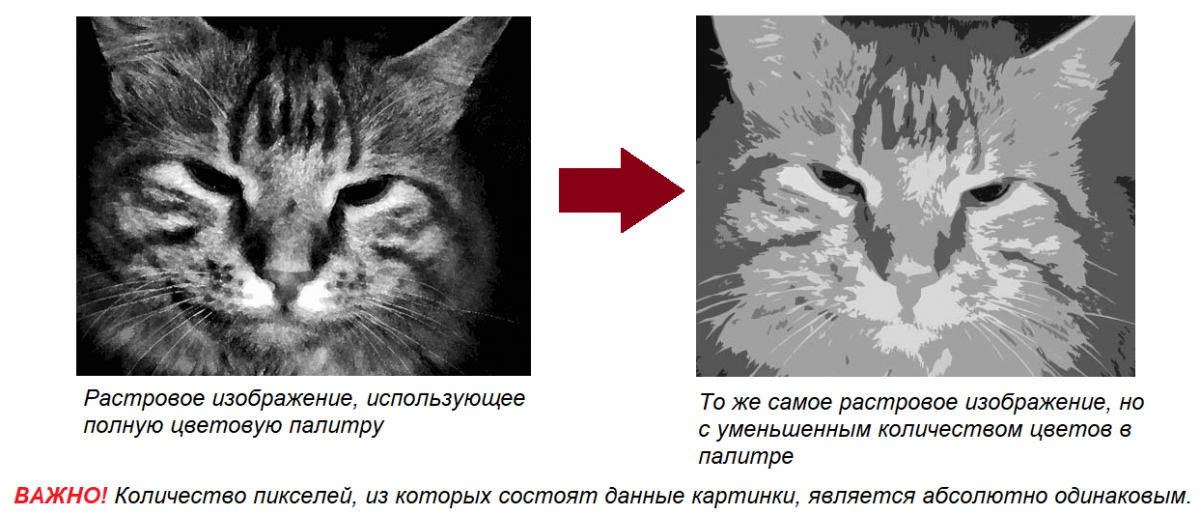
Также нам известно, что в процессе обработки картинки изменилась лишь цветовая палитра, а именно - было уменьшено количество цветов. В результате такой обработки информационный вес графического файла уменьшился.
А теперь внимание!![]() Важнейший момент в решении. Поймете его - легко сможете решать подобные примеры.
Важнейший момент в решении. Поймете его - легко сможете решать подобные примеры.
| Изменение количества используемых цветов в изображении никак не сказывается на его габаритах, а лишь на информационном весе! |
Это означает, что после преобразования количество пикселей, из которых состоит файл, осталось таким же, как и до преобразования. Поняв этот момент, дальнейшее решение, ну, лично у меня, уже не вызывает никаких трудностей.
Чтобы найти вес графического файла, нам хоть как придется прибегать к пиксельной матрице, поэтому, давайте обозначим за X количество пикселов, из которых состоят графические файлы.
Давайте проведем анализ исходного графического файла, т е файла, использующего $256$-цветовую палитру. Сходу можно найти глубину цвета по формуле Хартли: $I = K · \log_2 N$, где:
| $N$ - мощность алфавита | $K$ - длина сообщения | $I$ - количество информации в сообщении в битах |
Давайте произведем адаптацию величин этой формулы Хартли под наш случай:
Под величиной $I$ понимают глубину цвета любого пикселя, выраженную в битах.
Под мощностью алфавита $N$ понимают максимальное количество цветов, в которые можно раскрасить любой пиксель некоторого растрового изображения. Т. е. $N = 256$.
Под длиной сообщения $K$ стоит понимать количество пикселей, которые участвуют в обработке. Кстати, в нашем случае, $K = 1$, т к структурно все пиксели однотипны.
Посчитаем глубину цвета для графического файла до его преобразования:
$I_{до} = 1 · log_2\ 256 = log_2\ 2^8 = 8$ [бит].
Несмотря на то, что в конечном итоге ответ нам нужно дать в [Кбайтах], оставим пока что единицы измрения [бит].
Запишем формулу, по которой можно отыскать размер исходного растрового файла: $V_{до} = 8 ·X$[бит].
Давайте проведем анализ преобразованного графического файла, т е файла, использующего $4$-цветовую палитру. Аналогично
прибегнем к формуле Хартли для нахождения качества цветопередачи: $I_{после} = 1 · log_2\ 4 = log_2\ 2^2 = 2$ [бит].
Вычислим информационный вес преобразованного графического файла: $V_{после} = 2 ·X$[бит].
![]() А сейчас пришла пора воспользоваться заключительный условием, чтобы составить некое линейное уравнение, решив которое
А сейчас пришла пора воспользоваться заключительный условием, чтобы составить некое линейное уравнение, решив которое
найдем X. В условии говорится, что после преобразования размер файла сократился на $18$ [Кбайт].
Но, также не стоит забывать все привести к единым единицам измерения, иначе будет грубая математическая ошибка. Размеры обоих файлов мы посчитали в [битах], поэтому данное сокращение, также переведем до [бит]: $18[Кбайт] = 18 · 2^{13}$ [бит].
А вот сейчас запишем линейное уравнение и решим его:
$V_{до} = V_{после} + 18[Кбайт]$
$8 · X[бит] = 2 · X[бит] + 18 · 2^{13}[бит]$, сократим все слагаемые на [бит]
$6 · X = 18 · 2^{13}$
$X = \frac{3\ ·\ 6\ ·\ 2^{13}}{6} = 3 · 2^{13}$ - количество пикселей, из которых состоят наши графические файлы.
Но это значение не является конечным ответом, т к нас просили отыскать не общее количество пикселей, а информационный размер исходного файла. Внимание! Именно исходного, а не преобразованного. Будьте внимательны на экзамене.![]()
$V_{до} = 8 · X[бит] = 8 · 3 · 2^{13} = 2^3 · 3 · 2^{13} = 3 · 2^{3 + 13} = 3 · 2^{16}[бит]$..
По условии просят ответ получить в [Кбайтах], следовательно, делим рассчитанную величину на $2^{13}$, т к именно столько [бит] содержится в $1$-ом [Кбайте]:
$V_{до} = 3 · 2^{16}[бит] = \frac{3\ ·\ 2^{16}}{2^{13}}[Кбайт] = 3 · 2^3[Кбайт] = 24[Кбайт]$
Именно это значение нам следует выписать в бланк ответов официального экзамена ЕГЭ по информатике. Выписывается только число без указаний каких-либо единиц измерения информации.
Ответ: $24$
Выводы
Тезисно пробежимся по ключевым моментам решения задачи:
Читать + перечитывать условие задания до тех пор, пока не будут понятны все мелочи.
Правильно определить вид компьютерной графики. В нашем примере рассматривались графические файлы растрового типа.
Знать назубок формулу Хартли. Дополнительно понимать тему "Измерение количества информации".
Знать наизусть степени двоек: $2^0\ ..\ 2^{20}$. Или хотя бы до $2^{16}$.
Знать назубок таблицу единиц измерения информации. Будет неловко и смешно на официальном экзамене ЕГЭ по информатике, если забудете, сколько [бит] в $1$-ом [Кбайте].

Уметь сопоставлять графические файлы между собой, т е уметь проводить так называмый "до/после" сравнительный анализ.
Это минимум того, о чем нужно помнить! А максимум? Ну, максимума как такового нет, т к в сфере информационных технологий можно совершенствоваться всю жизнь.![]()
Примеры условий реальных задач, встречающихся на ЕГЭ по информатике
чуть позже!
На своих уроках делаю упор исключительно на практику! Никакой воды - только решения!
Вот и подошла к своему логическому завершению очередная статья, очередной разбор конкретного примера на кодирование графической информации.
Если остались вопросы, какие-то недопонимания, то у вас есть несколько путей решения:
написать комментарий под этой статьей, задав свой вопрос;
записаться ко мне на индивидуальную подготовку;
задать свой вопрос в моей персональной группе в вк;
написать мне на электронный адрес;
ничего не делать и ждать провала на рубежном экзамене ЕГЭ по информатике.

Если имеется свободных $2-3$ минутки, то можете познакомиться с отзывами моих учеников. Все они добились поставленных целей и стали значительно лучше разбираться в информационных технологиях.
Главный лейтмотив моих занятий - качественное решение как можно большего числа заданий. ЕГЭ - тестовый экзамен, поэтому практика, практика и еще раз только практика!
Отзывы
моих учеников

Орлов
Максим

Владимир
Дятлов

Маслова

Воробьев
Станислав

Догаев
Самир

Фрунзе
Яна

Малышев
Евгений

Крылов
Антон

Даниил
Сафонов

Дмитрий
Чуков

Мельник
Игорь

Дмитров
Анатолий





 Закажите звонок
Закажите звонок Смотрите отзывы
Смотрите отзывы Напишите письмо
Напишите письмо Закажите работу
Закажите работу